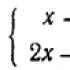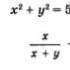Уравнения с двумя переменными (неопределенные уравнения). Системы уравнений. Основные понятия — Гипермаркет знаний Рациональные уравнения с двумя переменными
Линейное уравнение – уравнение вида a x = b , где x — переменная, a и b некоторые числа, причем a ≠ 0 .
Примеры:
- 3 x = 2
- 2 7 x = − 5
Линейными уравнениями называют не только уравнения вида a x = b , но и любые уравнения, которые при помощи преобразований и упрощений сводятся к этому виду.
Как же решать уравнения, которые приведены к виду a x = b ? Достаточно поделить левую и правую часть уравнения на величину a . В результате получим ответ: x = b a .
Как распознать, является ли произвольное уравнение линейным или нет? Надо обратить внимание на переменную, которая присутствует в нем. Если старшая степень, в которой стоит переменная, равна единице, то такое уравнение линейное.
Для того, чтобы решить линейное уравнение , необходимо раскрыть скобки (если они есть), перенести «иксы» в левую часть, числа – в правую, привести подобные слагаемые. Получится уравнение вида a x = b . Решение данного уравнения: x = b a .
Примеры:
- 2 x + 1 = 2 (x − 3) + 8
Это линейное уравнение, так как переменная стоит в первое степени.
Попробуем преобразовать его к виду a x = b:
Для начала раскроем скобки:
2 x + 1 = 4 x − 6 + 8
В левую часть переносятся все слагаемые с x , в правую – числа:
2 x − 4 x = 2 − 1
Теперь поделим левую и правую часть на число (-2) :
− 2 x − 2 = 1 − 2 = − 1 2 = − 0,5
Ответ: x = − 0,5
- x 2 − 1 = 0
Это уравнение не является линейным, так как старшая степень, в которой стоит переменная x равна двум.
- x (x + 3) − 8 = x − 1
Это уравнение выглядит линейным на первый взгляд, но после раскрытия скобок старшая степень становится равна двум:
x 2 + 3 x − 8 = x − 1
Это уравнение не является линейным.
Особые случаи (в 4 задании ОГЭ они не встречались, но знать их полезно)
Примеры:
- 2 x − 4 = 2 (x − 2)
2 x − 4 = 2 x − 4
2 x − 2 x = − 4 + 4
И как же здесь искать x , если его нет? После выполнения преобразований мы получили верное равенство (тождество), которое не зависит от значения переменной x . Какое бы значение x мы ни подставляли бы в исходное уравнение, в результате всегда получается верное равенство (тождество). Значит x может быть любым числом.
Ответ: x ∈ (− ∞ ; + ∞)
- 2 x − 4 = 2 (x − 8)
Это линейное уравнение. Раскроем скобки, перенесем иксы влево, числа вправо:
2 x − 4 = 2 x − 16
2 x − 2 x = − 16 + 4
В результате преобразований x сократился, но в итоге получилось неверное равенство, так как. Какое бы значение x мы ни подставляли бы в исходное уравнение, в результате всегда будет неверное равенство. А это означает, что нет таких значений x , при которых равенство становилось бы верным.
Вы уже встречались в курсе алгебры 7-го класса, но это были только системы специального вида - системы двух линейных уравнений с двумя переменными. В 8-м классе вы научились решать рациональные уравнения с одной переменной, значит, можно подумать и о решении систем рациональных уравнений с двумя переменными, тем более что такие системы довольно часто представляют собой математические модели изучаемых ситуаций. Об одной из таких моделей вы уже узнали из учебника «Алгебра-8». Приведенный ниже пример заимствован из указанного учебника.
На практике удобнее более широкое истолкование термина «рациональное уравнение с двумя переменными»: это уравнение вида - рациональные выражения с двумя переменными х и у.
Примеры рациональных уравнений с двумя переменными:

Конечно, можно рассматривать рациональные уравнения и с другими переменными, не обязательно с х ну, например, а3 - bx = = 3аb - рациональное уравнение с двумя переменными а, b. Но по традиции в алгебре предпочитают в качестве переменных использовать буквы х, у.
Определение 2.
Решением уравнения р (х, у) = 0 называют всякую пару чисел (х;у), которая удовлетворяет этому уравнению, т.е. обращает равенство с переменными р (х, у) = 0 в верное числовое равенство.
Например:
1) (3; 7) - решение уравнения х 2 + у 2 = 58. В самом деле, З 2 + 7 2 = 58 - верное числовое равенство.
2) - решение уравнения х 2 + у 2 - 58. В самом деле, ![]() - верное числовое равенство (22 + 36 = 58).
- верное числовое равенство (22 + 36 = 58).
3) (0; 5) - решение уравнения 2ху + х 3 = 0. В самом деле, 2 0 5 + 0+ О 2 = 0 - верное числовое равенство.
4) (1; 2) не является решением уравнения 2ху + х 3 = 0. В самом деле, 2 1 2 + 3 = 0 - неверное равенство (получается 5 = 0).
Для уравнений с двумя переменными, как и для уравнений с одной переменной, можно ввести понятие равносильности уравнений.
Определение 3.
Два уравнения р(х, у) = 0 и д(х, у) = 0 называют равносильными, если они имеют одинаковые решения (в частности, если оба уравнения не имеют решений).
Обычно при решении уравнения стараются заменить данное уравнение более простым, но равносильным ему. Такую замену называют равносильным преобразованием уравнения. Два основных равносильных преобразования указаны ниже:
1) Перенос членов уравнения из одной части уравнения в другую с противоположными знаками.
Например, замена уравнения 2х + bу = 7х - 8у уравнением 2х - 7х - -8у - bу есть равносильное преобразование уравнения.
2) Умножение или деление обеих частей уравнения на одно и то же отличное от нуля число или выражение.
Например, замена уравнения 0,5л:2 - 0,3ху = 2у уравнением 5л:2 - 3ху = 20у (обе части уравнения умножили почленно на 10) есть равносильное преобразование уравнения.
Неравносильными преобразованиями уравнения, как и в случае уравнений с одной переменной, являются:
1) Освобождение от знаменателей, содержащих переменные.
2) Возведение обеих частей уравнения в квадрат.
Если в процессе решения уравнения применялось одно из указанных неравносильных преобразований, то все найденные решения надо проверить подстановкой в исходное уравнение, поскольку среди них могут оказаться посторонние решения.
Иногда удается перейти к геометрической (графической) модели уравнения с двумя переменными, т.е. построить график уравнения. Вы, наверное, помните, что графиком линейного уравнения с двумя переменными ах + bу + с = 0 (а, Ь, с - числа, коэффициенты, где хотя бы одно из чисел а, Ь отлично от нуля) является прямая линия - геометрическая модель линейного уравнения. Попробуем найти соответствующие графические модели еще для некоторых рациональных уравнений с двумя переменными х и у.
Пример 2. Построить график уравнения у - 2х2 = 0.
Решение. Преобразуем уравнение к виду у = 2х2. Графиком функции у - 2х2 является парабола, она же считается графиком уравнения у - 2х2 = 0 (рис. 33).
Пример 3.
Построить график уравнения ху = 2.
Решение.
Преобразуем уравнение к виду Графиком функции - является гипербола, она же считается графиком уравнения ху = 2 (рис. 34).

Таким образом, если уравнение р(х, у) = О удается преобразовать к виду у = f (x), то график функции у - f (х) считается одновременно и графиком уравнения р(х, у) - 0.
Пример 4. Построить график уравнения х 2 + у 2 = 16.
Решение.
Воспользуемся теоремой из курса геометрии: графиком уравнения х 2 + у 2 = г 2 , где r- положительное число, является окружность с центром в начале координат и радиусом r. Значит, графиком уравнения х 2 + у 2 = 16 является окружность с центром в начале координат и радиусом 4 (рис. 35).
Упомянутая выше теорема является частным случаем следующей теоремы , которая, надеемся, также известна вам из курса геометрии.


Пример 5.
Построить график уравнения:
а) (х - I) 2 + (у - 2) 2 = 9; б) х 2 + у 2 + 4х= 0.
Решение:
а) Перепишем уравнение в виде (x - I) 2 + (у - 2) 2 = З2. Графиком этого уравнения, по теореме, является окружность с центром в точке (1; 2) и радиусом 3 (рис. 37).
б) Перепишем уравнение в виде (х 2 + 4х + 4) + у 2 = 4, т.е. (х + 2) 2 + у 2 = 4 и далее (х - (-2)) 2 + (у - О) 2 = 22. Графиком этого уравнения, по теореме, является окружность с центром в точке (-2; 0) и радиусом 2 (рис. 38).
Определение 4.
Если поставлена задача найти такие пары значений (х; у), которые одновременно удовлетворяют уравнению р (х, у) = 0 и уравнению q (х, у) = 0, то говорят, что указанные уравнения образуют систему уравнений:

Пару значений (х; у), которая одновременно является решением и первого и второго уравнений системы, называют решением системы уравнений. Решить систему уравнений - это значит найти все ее решения или установить, что решений нет.
Например, пара (3; 7) - решение системы уравнений

В самом деле, эта пара удовлетворяет как первому, так и второму уравнению системы, значит, является ее решением. Обычно пишут так: (3; 7) - решение системы или A пара (5; 9) не является решением системы (1): она не удовлетворяет первому уравнению (хотя и удовлетворяет второму уравнению системы).
Разумеется, переменные в уравнениях, образующих систему уравнений, могут быть обозначены и другими буквами, например: Но в любом случае при записи ответа в виде пары чисел используют лексикографический метод, т.е. на первое место ставят ту из двух букв, которая в латинском алфавите встречается раньше.
Иногда удается решить систему уравнений графическим методом, с которым вы знакомы: надо построить график первого уравнения, затем построить график второго уравнения и, наконец, найти точки пересечения графиков ; координаты каждой точки пересечения служат решением системы уравнений.
Пример 6. Решить систему уравнений

Решение.
1) Построим график уравнения х 2 + у 2 = 16 - окружность с центром в начале координат и радиусом 4 (рис. 39).
2) Построим график уравнения у - х = 4. Это прямая, проходящая через точки (0; 4) и (-4; 0) (рис. 39).
3) Окружность и прямая пересекаются в точках А и В (рис. 39). Судя по построенной геометрической модели, точка A имеет координаты А(-4; 0), а точка В - координаты В(0; 4). Проверка показывает, что на самом деле пара (-4; 0) и пара (0; 4) являются решениями обоих уравнений системы, а значит, и решениями системы уравнений. Следовательно, заданная система уравнений имеет два решения: (-4; 0) и (0; 4).
Ответ: (-4; 0); (0; 4).
Пример 7. Решить систему уравнений
Решение.
1) Переписав первое уравнение системы в виде у = 2х 2 , приходим к выводу: графиком уравнения является парабола (рис. 40).
2) Переписав второе уравнение системы в виде приходим к выводу: графиком уравнения является гипербола (рис. 40).

3) Парабола и гипербола пересекаются в точке А (рис. 40). Судя по построенной геометрической модели, точка A имеет координаты A (1; 2). Проверка показывает, что действительно пара (1; 2) является решением обоих уравнений системы, а значит, и решением системы уравнений. Следовательно, заданная система уравнений имеет одно решение: (1; 2).
Ответ: (1; 2).
Графический метод решения систем уравнений, как и графический метод решения уравнений, красив, но ненадежен: во-первых, потому, что графики уравнений мы сумеем построить далеко не всегда; во-вторых, даже если графики уравнений удалось построить, точки пересечения могут быть не такими «хорошими», как в специально подобранных примерах 6 и 7, а то и вовсе могут оказаться за пределами чертежа. Значит, нам нужно располагать надежными алгебраическими методами решения систем двух уравнений с двумя переменными. Об этом и пойдет речь в следующем параграфе.
А.Г. Мордкович Алгебра 9 класс
Материалы по математике онлайн , задачи и ответы по классам, планы конспектов уроков по математике
Наименьший общий знаменатель используется для упрощения данного уравнения. Этот метод применяется в том случае, когда вы не можете записать данное уравнение с одним рациональным выражением на каждой стороне уравнения (и воспользоваться методом умножения крест-накрест). Этот метод используется, когда вам дано рациональное уравнение с 3 или более дробями (в случае двух дробей лучше применить умножение крест-накрест).
Найдите наименьший общий знаменатель дробей (или наименьшее общее кратное). НОЗ – это наименьшее число, которое делится нацело на каждый знаменатель.
- Иногда НОЗ – очевидное число. Например, если дано уравнение: х/3 + 1/2 = (3x +1)/6, то очевидно, что наименьшим общим кратным для чисел 3, 2 и 6 будет 6.
- Если НОЗ не очевиден, выпишите кратные самого большого знаменателя и найдите среди них такой, который будет кратным и для других знаменателей. Зачастую НОЗ можно найти, просто перемножив два знаменателя. Например, если дано уравнение x/8 + 2/6 = (x - 3)/9, то НОЗ = 8*9 = 72.
- Если один или несколько знаменателей содержат переменную, то процесс несколько усложняется (но не становится невозможным). В этом случае НОЗ представляет собой выражение (содержащее переменную), которое делится на каждый знаменатель. Например, в уравнении 5/(х-1) = 1/х + 2/(3x) НОЗ = 3x(х-1), потому что это выражение делится на каждый знаменатель: 3x(х-1)/(х-1) = 3x; 3x(х-1)/3х = (х-1); 3x(х-1)/х = 3(х-1).
Умножьте и числитель, и знаменатель каждой дроби на число, равное результату деления НОЗ на соответствующий знаменатель каждой дроби. Так как вы умножаете и числитель, и знаменатель на одно и тоже число, то фактически вы умножаете дробь на 1 (например, 2/2 = 1 или 3/3 = 1).
- Таким образом, в нашем примере умножьте х/3 на 2/2, чтобы получить 2x/6, и 1/2 умножьте на 3/3, чтобы получить 3/6 (дробь 3x +1/6 умножать не надо, так как ее знаменатель равен 6).
- Действуйте аналогично в случае, когда переменная находится в знаменателе. В нашем втором примере НОЗ = 3x(x-1), поэтому 5/(x-1) умножьте на (3x)/(3x) и получите 5(3x)/(3x)(x-1); 1/x умножьте на 3(x-1)/3(x-1) и получите 3(x-1)/3x(x-1); 2/(3x) умножьте на (x-1)/(x-1) и получите 2(x-1)/3x(x-1).
Найдите х. Теперь, когда вы привели дроби к общему знаменателю, вы можете избавиться от знаменателя. Для этого умножьте каждую сторону уравнения на общий знаменатель. Затем решите полученное уравнение, то есть найдите «х». Для этого обособьте переменную на одной из сторон уравнения.
- В нашем примере: 2x/6 + 3/6 = (3x +1)/6. Вы можете сложить 2 дроби с одинаковым знаменателем, поэтому запишите уравнение как: (2x+3)/6=(3x+1)/6. Умножьте обе части уравнения на 6 и избавьтесь от знаменателей: 2x+3 = 3x +1. Решите и получите х = 2.
- В нашем втором примере (с переменной в знаменателе) уравнение имеет вид (после приведения к общему знаменателю): 5(3x)/(3x)(x-1) = 3(x-1)/3x(x-1) + 2(x-1)/3x(x-1). Умножив обе стороны уравнения на НОЗ, вы избавитесь от знаменателя и получите: 5(3x) = 3(х-1) + 2(х-1), или 15x = 3x - 3 + 2x -2, или 15х = х - 5. Решите и получите: х = -5/14.
549+45у+4у=-7, 45у+4у=549-7, 49у=542, у=542:49, у≈11.
В произвольно выбранное (из системы) уравнение вставить вместо уже найденного «игрека» число 11 и вычислить второе неизвестное:
Х=61+5*11, х=61+55, х=116.
Ответ данной системы уравнений: х=116, у=11.
Графический способ.
Заключается в практическом нахождении координаты точки, в которой пересекаются прямые, математически записанные в системе уравнений. Следует начертить графики обоих прямых по отдельности в одной системе координат. Общий вид уравнения прямой: – у=kх+b. Чтобы построить прямую, достаточно найти координаты двух точек, причем, х выбирается произвольно.
Пусть дана система: 2х – у=4
У=-3х+1.
Строится прямая по первому уравнению, для удобства его нужно записать: у=2х-4. Придумать (полегче) значения для икс, подставляя его в уравнение, решив его, найти игрек. Получаются две точки, по которым строится прямая. (см рис.)
х 0 1
у -4 -2
Строится прямая по второму уравнению: у=-3х+1.
Так же построить прямую. (см рис.)
у 1 -5
Найти координаты точки пересечения двух построенных прямых на графике (если прямые не пересекаются, то система уравнений не имеет решения – так бывает).
Видео по теме
Полезный совет
Если одну и ту же систему уравнений решить тремя разными способами, ответ получится одинаковый (если решение верно).
Источники:
- Алгебра 8 класса
- решить уравнение с двумя неизвестными онлайн
- Примеры решения систем линейных уравнений с двумя
Решение системы уравнений сложно и увлекательно. Чем сложнее система, тем интереснее ее решать. Чаще всего в математике средней школы встречаются системы уравнений с двумя неизвестными, но в высшей математике переменных может быть и больше. Решать системы можно несколькими методами.
Инструкция
Самый распространенный метод решения системы уравнений - это подстановка. Для этого необходимо выразить одну переменную через другую и подставить ее во второе уравнение системы, таким образом приведя уравнение к одной переменной. Например, дана уравнений:2х-3у-1=0;х+у-3=0.
Из второго выражения удобно выразить одну из переменных, перенеся все остальное в правую часть выражения, не забыв при этом сменить знак коэффициента:х=3-у.
Раскрываем скобки: 6-2у-3у-1=0;-5у+5=0;у=1.Полученное значение у подставляем в выражение:х=3-у;х=3-1;х=2.
В первом выражении все члены 2, можно вынести 2 за скобку
Обращение автора к данной теме не является случайным. Уравнения с двумя переменными впервые встречаются в курсе 7-го класса. Одно уравнение с двумя переменными имеет бесконечное множество решений. Это наглядно демонстрирует график линейной функции, заданный в виде ax + by=c. В школьном курсе учащиеся изучают системы двух уравнений с двумя переменными. В результате из поля зрения учителя и, поэтому ученика, выпадает целый ряд задач, с ограниченными условиями на коэффициент уравнения, а также методы их решения.
Речь идет о решении уравнения с двумя неизвестными в целых или натуральных числах.
В школе натуральные и целые числа изучаются в 4-6-х классах. К моменту окончания школы не все ученики помнят различия между множествами этих чисел.
Однако задача типа “решить уравнение вида ax + by=c в целых числах” все чаще встречается на вступительных экзаменах в ВУЗы и в материалах ЕГЭ.
Решение неопределенных уравнений развивает логическое мышление, сообразительность, внимание анализировать.
Я предлагаю разработку нескольких уроков по данной теме. У меня нет однозначных рекомендаций по срокам проведения этих уроков. Отдельные элементы можно использовать и в 7-м классе (для сильного класса). Данные уроки можно взять за основу и разработать небольшой элективный курс по предпрофильной подготовке в 9-м классе. И, конечно, этот материал можно использовать в 10-11 классах для подготовки к экзаменам.
Цель урока:
- повторение и обобщение знаний по теме “Уравнения первого и второго порядка”
- воспитание познавательного интереса к учебному предмету
- формирование умений анализировать, проводить обобщения, переносить знания в новую ситуацию
Урок 1.
Ход урока.
1) Орг. момент.
2) Актуализация опорных знаний.
Определение. Линейным уравнением с двумя переменными называется уравнение вида
mx + ny = k, где m, n, k – числа, x, y – переменные.
Пример: 5x+2y=10
Определение. Решением уравнения с двумя переменными называется пара значений переменных, обращающая это уравнение в верное равенство.
Уравнения с двумя переменными, имеющими одни и те же решения, называются равносильными.
1. 5x+2y=12 (2)y = -2.5x+6
Данное уравнение может иметь сколько угодно решений. Для этого достаточно взять любое значение x и найти соответствующее ему значение y.
Пусть x = 2, y = -2.5 2+6 = 1
x = 4, y = -2.5 4+6 =- 4
Пары чисел (2;1); (4;-4) – решения уравнения (1).
Данное уравнение имеет бесконечно много решений.
3) Историческая справка
Неопределенные (диофантовы) уравнения – это уравнения, содержащие более одной переменной.
В III в. н.э. – Диофант Александрийский написал “Арифметику”, в которой расширил множество чисел до рациональных, ввел алгебраическую символику.
Так же Диофант рассмотрел проблемы решения неопределенных уравнений и им даны методы решения неопределенных уравнений второй и третьей степени.
4) Изучение нового материала.
Определение: Неоднородным диофантовым уравнением первого порядка с двумя неизвестными x, y называется уравнение вида mx + ny = k, где m, n, k, x, y Z k0
Утверждение 1.
Если свободный член k в уравнении (1) не делится на наибольший общий делитель (НОД) чисел m и n, то уравнение (1) не имеет целых решений.
Пример: 34x – 17y = 3.
НОД (34; 17) = 17, 3 не делится нацело на 17, в целых числах решения нет.
Пусть k делится на НОД (m, n). Делением всех коэффициентов можно добиться, что m и n станут взаимно простыми.
Утверждение 2.
Если m и n уравнения (1) взаимно простые числа, то это уравнение имеет по крайней мере одно решение.
Утверждение 3.
Если коэффициенты m и n уравнения (1) являются взаимно простыми числами, то это уравнение имеет бесконечно много решений:
Где (; ) – какое-либо решение уравнения (1), t Z
Определение. Однородным диофантовым уравнением первого порядка с двумя неизвестными x, y называется уравнение вида mx + ny = 0, где (2)
Утверждение 4.
Если m и n – взаимно простые числа, то всякое
решение уравнения (2) имеет вид ![]()
5) Домашнее задание. Решить уравнение в целых числах:
- 9x – 18y = 5
- x + y= xy
- Несколько детей собирали яблоки. Каждый мальчик собрал по 21 кг, а девочка по 15 кг. Всего они собрали 174 кг. Сколько мальчиков и сколько девочек собирали яблоки?
Замечание. На данном уроке не представлены примеры решения уравнений в целых числах. Поэтому домашнее задание дети решают исходя из утверждения 1 и подбором.
Урок 2.
1) Организационный момент
2) Проверка домашнего задания
1) 9x – 18y = 5
5 не делится нацело на 9, в целых числах решений нет.
Методом подбора можно найти решение
Ответ: (0;0), (2;2)
3) Составим уравнение:
Пусть мальчиков x, x Z, а девочек у, y Z, то можно составить уравнение 21x + 15y = 174
Многие учащиеся, составив уравнение, не смогут его решить.
Ответ: мальчиков 4, девочек 6.
3) Изучение нового материала
Столкнувшись с трудностями при выполнении домашнего задания, учащиеся убедились в необходимости изучения их методов решений неопределенных уравнений. Рассмотрим некоторые из них.
I. Метод рассмотрения остатков от деления.
Пример. Решить уравнение в целых числах 3x – 4y = 1.
Левая часть уравнения делится на 3, следовательно, должна делиться и правая часть. Рассмотрим три случая.
Ответ: где m Z.
Описанный метод удобно применять в случае, если числа m и n не малы, но зато разлагаются на простые сомножители.
Пример: Решить уравнения в целых числах.
Пусть y = 4n, тогда 16 - 7y = 16 – 7 4n = 16 – 28n = 4*(4-7n) делится на 4.
y = 4n+1, тогда 16 – 7y = 16 – 7 (4n + 1) = 16 – 28n – 7 = 9 – 28n не делится на 4.
y = 4n+2, тогда 16 – 7y = 16 – 7 (4n + 2) = 16 – 28n – 14 = 2 – 28n не делится на 4.
y = 4n+3, тогда 16 – 7y = 16 – 7 (4n + 3) = 16 – 28n – 21 = -5 – 28n не делится на 4.
Следовательно, y = 4n, тогда
4x = 16 – 7 4n = 16 – 28n, x = 4 – 7n
Ответ: , где n Z.
II. Неопределенные уравнения 2-ой степени
Сегодня на уроке мы лишь коснемся решения диофантовых уравнений второго порядка.
И из всех типов уравнений рассмотрим случай, когда можно применить формулу разности квадратов или другой способ разложения на множители.
Пример: Решить уравнение в целых числах.
![]()
13 – простое число, поэтому оно может быть разложено на множители лишь четырьмя способами: 13 = 13 1 = 1 13 = (-1)(-13) = (-13)(-1)
Рассмотрим эти случаи
Ответ: (7;-3), (7;3), (-7;3), (-7;-3).
4) Домашнее задание.
Примеры. Решить уравнение в целых числах:
(x - y)(x + y)=4
| 2x = 4 | 2x = 5 | 2x = 5 |
| x = 2 | x = 5/2 | x = 5/2 |
| y = 0 | не подходит | не подходит |
| 2x = -4 | не подходит | не подходит |
| x = -2 | ||
| y = 0 |
Ответ: (-2;0), (2;0).
Ответы: (-10;9), (-5;3), (-2;-3), (-1;-9), (1;9), (2;3), (5;-3), (10;-9).
в) ![]()
Ответ: (2;-3), (-1;-1), (-4;0), (2;2), (-1;3), (-4;5).
Итоги. Чтозначит решить уравнение в целых числах?
Какие методы решения неопределенных уравнений вы знаете?
Приложение:
Упражнения для тренировки.
1) Решите в целых числах.
| а) 8x + 12y = 32 | x = 1 + 3n, y = 2 - 2n, n Z |
| б) 7x + 5y = 29 | x = 2 + 5n, y = 3 – 7n, n Z |
| в) 4x + 7y = 75 | x = 3 + 7n, y = 9 – 4n, n Z |
| г) 9x – 2y = 1 | x = 1 – 2m, y = 4 + 9m, m Z |
| д) 9x – 11y = 36 | x = 4 + 11n, y = 9n, n Z |
| е) 7x – 4y = 29 | x = 3 + 4n, y = -2 + 7n, n Z |
| ж) 19x – 5y = 119 | x = 1 + 5p, y = -20 + 19p, p Z |
| з) 28x – 40y = 60 | x = 45 + 10t, y = 30 + 7t, t Z |
2) Найти целые неотрицательные решения уравнения:
Решение:Z (2; -1)
Литература.
- Детская энциклопедия “Педагогика”, Москва, 1972 г.
- Алгебра-8, Н.Я. Виленкин, ВО “Наука”, Новосибирск, 1992 г.
- Конкурсные задачи, основанные на теории чисел. В.Я. Галкин, Д.Ю. Сычугов. МГУ, ВМК, Москва, 2005г.
- Задачи повышенной трудности в курсе алгебры 7-9 классов. Н.П. Косрыкина. “Просвещение”, Москва, 1991 г.
- Алгебра 7, Макарычев Ю.Н., “Просвещение”.