Вращательное движение тела. Закон вращательного движения. Динамика вращательного движения Любая ли сила вызывает вращательное движение

При наблюдении сложных движений, например движения тела человека (ходьба, бег, прыжки и т.д.), кажется трудным или даже невозможным описать перемещение всех его точек. Однако, анализируя такие движения, можно заметить, что они состоят из более простых - поступательных и вращательных перемещений.

Механика поступательного движения известна читателю, поэтому раздел начинается с рассмотрения вращательного движения. Наиболее простым является вращение твердого тела вокруг неподвижной оси. Этот случай позволяет ознакомиться со спецификой, терминологией и законами вращательного движения.

5.1. КИНЕМАТИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ АБСОЛЮТНО ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ОСИ

Абсолютно твердым телом называют такое, расстояние между любыми двумя точками которого неизменно.

Размеры и форма абсолютно твердого тела не изменяются при его движении.

Понятие «абсолютно твердое тело» - физическая абстракция, так как любое тело способно к деформациям. Однако во многих случаях деформацией можно пренебречь.

Наиболее простой случай вращательного движения абсолютно твердого тела - вращение относительно неподвижной оси. Это такое движение, при котором точки тела движутся по окружностям, центры которых лежат на прямой, называемой осью вращения.

Известно, что в некоторых случаях для характеристики движения тела необязательно указывать движение всех его точек; так, например, при поступательном движении достаточно указать движение любой одной точки тела.

При вращательном движении вокруг оси точки тела перемещаются по разным траекториям, но за одно и то же время все точки и само тело поворачивается на одинаковый угол. Для характеристики вращения

проведем в плоскости, перпендикулярной оси, радиус-вектор к некоторой точке i (рис. 5.1). Временная зависимость угла α поворота радиуса-вектора относительно некоторого выделенного направления ОХ является уравнением вращательного движения твердого тела вокруг неподвижной оси:

Быстрота вращения тела характеризуется угловой скоростью, равной первой производной от угла поворота радиуса-вектора по времени:

Угловая скорость есть вектор, который направлен по оси вращения и связан с направлением вращения правилом правого винта (рис. 5.2). Вектор угловой скорости в отличие от векторов скорости и силы является скользящим: у него нет определенной точки приложения, и он может быть расположен в любом месте на оси вращения. Таким образом, задание вектора ω указывает положение оси вращения, направление вращения и модуль угловой скорости.

Быстрота изменения угловой скорости характеризуется угловым ускорением, равным первой производной от угловой скорости по времени:

или в векторной форме:

Из (5.4) видно, что вектор углового ускорения совпадает по направлению с элементарным, достаточно малым изменением вектора угловой скорости dω : при ускоренном вращении угловое ускорение направлено так же, как и угловая скорость, при замедленном вращении - противоположно ей.

Так как угловое перемещение всех точек абсолютно твердого тела одинаково, то, согласно (5.2) и (5.3), одновременно все точки тела имеют одинаковую угловую скорость и одинаковое угловое ускорение. Линейные характеристики - перемещение, скорость, ускорение - различны для разных точек. Укажем в скалярном виде связь, которая может быть выведена самостоятельно, между линейными и угловыми характеристиками для i-й точки, движущейся по окружности радиусом r i:

Рис. 5.3

В заключение приведем полученные путем интегрирования соответствующих выражений формулы кинематики вращательного движения твердого тела вокруг неподвижной оси:

уравнение равномерного вращательного движения [см. (5.2)]:

зависимость угловой скорости от времени в равнопеременном вращательном движении [см. (5.3)]:

уравнение равнопеременного вращательного движения [см. (5.1) и (5.6)]:

Полезно сопоставить эти формулы с аналогичными зависимостями для поступательного движения.

5.2. ОСНОВНЫЕ ПОНЯТИЯ. УРАВНЕНИЕ ДИНАМИКИ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ

Момент силы _

Пусть к некоторой точке i твердого тела приложена сила F^, лежащая в плоскости, перпендикулярной оси вращения (рис. 5.4).

Моментом силы относительно оси вращения называют векторное произведение радиуса-вектора точки i на силу:

Раскрывая его, можно записать:

где β - угол между векторами r i и F i . Так как плечо силы h i = r i sinβ (см. рис. 5.4), то

Если сила действует под некоторым углом α к плоскости вращения (рис. 5.5), то ее можно разложить на две составляющие. Одна из них лежит в плоскости, перпендикулярной оси вращения, а другая параллельна этой этой оси и не оказывает влияния на вращение тела (в реальном случае она действует лишь на подшипники). Далее будут рассматриваться только силы, лежащие в плоскости, перпендикулярной оси вращения.

Рис. 5.4

Рис. 5.5

Работа во вращательном движении

Пусть при действии силы F i (см. рис. 5.4) тело поворачивается на достаточно малый угол dα. Найдем работу этой силы.

Известное из средней школы выражение для работы силы в данном случае следует записать так:

Итак,

элементарная работа силы во вращательном движении равна произведению момента силы на элементарный угол поворота тела.

Если на тело действует несколько сил, то элементарная работа, совершенная всеми ими, определяется аналогично (5.12):

где М - суммарный момент всех внешних сил, действующих на тело.

Если при повороте тела положение радиуса-вектора изменилось от α 1 до α 2 , то работа внешних сил может быть найдена интегрированием выражения (5.13):

Момент инерции

Мерой инертности тел при поступательном движении является масса. Инертность тел при вращательном движении зависит не только от массы, но и от распределения ее в пространстве относительно оси. Мера инертности тела при вращении характеризуется моментом инерции тела относительно оси вращения. Укажем сначала, что

моментом инерции материальной точки относительно оси вращения называют величину, равную произведению массы точки на квадрат расстояния ее от оси:

Моментом инерции тела относительно оси называют сумму моментов инерции всех материальных точек, из которых состоит тело:

В качестве примера выведем формулу момента инерции тонкого однородного стержня длиной l и массой т относительно оси, перпендикулярной стержню и проходящей через его середину (рис. 5.6). Выберем достаточно малый участок стержня длиной dx и массой dm, удаленный от оси 00" на расстояние х. Ввиду малости этого участка он может быть принят за материальную точку, его момент инерции [см. (5.15)] равен:

Масса элементарного участка равна произведению линейной плотности т/l, умноженной на длину элементарного участка: dm = (m/l) dx Подставив это выражение в (5.18), получим

Чтобы найти момент инерции всего стержня, проинтегрируем выражение (5.19) по всему стержню, т.е. в пределах от -1/2 до +1/2:

Приведем выражения для моментов инерции разных симметричных тел массой т:

полого однородного цилиндра (обруча) с внутренним радиусом r и внешним R относительно оси ОО", совпадающей с геометрической осью цилиндра (рис. 5.7):

сплошного однородного цилиндра (r = 0) или диска [см. (5.21)]:

однородного шара относительно оси, проходящей через его центр:

прямоугольною параллелепипеда относительно оси ОО", проходящей через его центр перпендикулярно плоскости основания (рис. 5.8):

Во всех перечисленных примерах ось вращения проходит через центр масс тела. При решении задач для определения момента инерции тела относительно оси, не проходящей через центр масс, можно воспользоваться теоремой Гюйгенса. Согласно этой теореме, момент инерции тела относительно некоторой оси OO":

где J 0 - момент инерции относительно параллельной оси, проходящей через центр масс тела OO"; т - масса тела; d - расстояние между двумя параллельными осями (рис. 5.9). Единицей момента инерции является килограмм-метр в квадрате (кг-м 2).

Момент импульса

Моментом импульса (момент количества движения) материальной точки, вращающейся относительно некоторой оси, называется величина, равная произведению импульса точки на расстоянии ее до оси вращения:

Момент импульса тела, вращающегося относительно некоторой оси, равен сумме моментов импульсов точек, из которых состоит данное тело:

Так как угловая скорость всех точек твердого тела одинакова, выне-ся ω за знак суммы [см. (5.29)], получим:

(/ - момент инерции тела относительно оси), или в векторной форме:

Итак, момент импульса равен произведению момента инерции точки на угловую скорость. Отсюда следует, что направления векторов момента импульса и угловой скорости совпадают. Единицей момента импульса является килограмм-метр в квадрате в секунду (кг? м 2 ? с -1).

Формулу (5.31) полезно сравнить с аналогичной формулой для импульса в поступательном движении.

Кинетическая энергия вращающегося тела

При вращении тела его кинетическая энергия складывается из кинетических энергий отдельных точек тела. Для твердого тела:

Полезно сопоставить выражение (5.32) с аналогичным выражением для поступательного движения.

Продифференцировав (5.32), получим элементарное изменение кинетической энергии во вращательном движении:

Основное уравнение динамики вращательного движения

Пусть твердое тело, на которое действовали внешние силы, повернулось на достаточно малый угол da. Приравняем элементарную работу всех внешних сил при таком повороте [см. (5.13)] элементарному изменению кинетической энергии [см. (5.33)]: M dα = J ω dω , откуда:

Это и есть основное уравнение динамики вращательного движения. Из (5.35) видно, что момент инерции характеризует инерционные свойства тела во вращательном движении: при действии внешних сил угловое ускорение тела тем больше, чем меньше момент инерции тела.

Основное уравнение для вращательного движения играет ту же роль, что и второй закон Ньютона для поступательного. Физические величины, входящие в это уравнение, аналогичны соответственно силе, массе и ускорению.

Из (5.34) следует, что:

Производная от момента импульса тела по времени равна равнодействующему моменту всех внешних сил.

Зависимость углового ускорения от момента силы и момента инерции можно продемонстрировать с по-

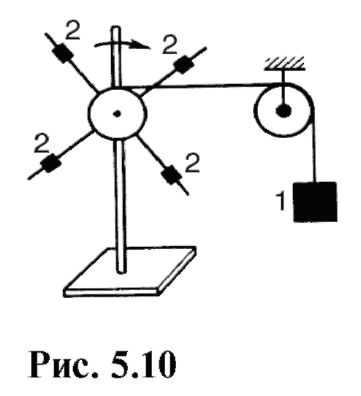
мощью прибора, изображенного на рис. 5.10. Под действием груза 1, подвешенного на нити, перекинутой через блок, крестовина ускоренно вращается. Перемещая грузики 2 на разные расстояния от оси вращения, можно изменять момент инерции крестовины. Меняя грузы, т.е. моменты сил, и момент инерции, можно убедиться, что угловое ускорение возрастает при увеличении момента силы или уменьшении момента инерции.

5.3. ЗАКОН СОХРАНЕНИЯ МОМЕНТА ИМПУЛЬСА

Рассмотрим частный случай вращательного движения, когда суммарный момент внешних сил равен нулю. Как видно из (5.37), dL/dt = 0 при М = 0, откуда

Это положение известно под названием закона сохранения момента импульса: если суммарный момент всех внешних сил, действующих на тело, равен нулю, то момент импульса этою тела остается постоянным.

Опуская доказательство, отметим, что закон сохранения момента импульса справедлив не только для абсолютно твердого тела.

Наиболее интересные применения этого закона связаны с вращением системы тел вокруг общей оси. При этом необходимо учитывать векторный характер момента импульса и угловых скоростей. Так, для системы, состоящей из N тел, вращающихся вокруг общей оси, закон сохранения момента импульса можно записать в форме:

Рассмотрим некоторые примеры, иллюстрирующие этот закон.

Гимнаст, выполняющий сальто (рис. 5.11), в начальной фазе сгибает колени и прижимает их к груди, уменьшая тем самым момент инерции и увеличивая угловую скорость вращения вокруг горизонтальной оси, проходящей через центр масс. В конце прыжка тело выпрямляется, момент инерции возрастает, угловая скорость уменьшается. Фигурист, совершающий вращение вокруг вертикальной оси (рис. 5.12), в начале вращения приближает руки к корпусу, тем самым уменьшая момент инерции и увеличивая угловую скорость. В конце вращения происходит обратный процесс: при разведении рук увеличивается момент инерции и уменьшается угловая скорость, что позволяет легко остановиться.

Такое же явление может быть продемонстрировано на скамье Жуковского, которая представляет собой легкую горизонтальную платформу, вращающуюся с малым трением вокруг вертикальной оси. При изменении положения рук изменяются момент инерции и угловая скорость (рис. 5.13), момент импульса остается постоянным. Для усиления демонстрационного эффекта в руках человека гантели. На скамье Жуковского можно продемонстрировать векторный характер закона сохранения момента импульса.

Экспериментатор, стоящий на неподвижной скамье, получает от помощника велосипедное колесо, вращающееся вокруг вертикальной оси (рис. 5.14, слева). В этом случае момент импульса системы человек и платформа-колесо определяется только моментом импульса колеса:

здесь J ч - момент инерции человека и платформы; J K и ω κ - момент инерции и угловая скорость колеса. Так как момент внешних сил относительно вертикальной оси равен нулю, то L сохраняется (L = const).

Если экспериментатор повернет ось вращения колеса на 180° (рис. 5.14, справа), то момент импульса колеса будет направлен противоположно первоначальному и равен J K ω K . Так как вектор момента импульса колеса изменяется, а момент импульса системы сохраняется, то неизбежно должен измениться и момент импульса, человека и платформы, он уже не будет равен нулю 1 . Момент импульса системы в этом случае

1 Небольшим несовпадением оси колеса с осью вращения платформы можно пренебречь.

По формуле (5.42) можно приближенно оценить момент инерции тела человека вместе с платформой, для чего необходимо измерить ω κ , ω 4 и найти J k . Способ измерения угловых скоростей равномерного вращения известен читателю. Зная массу колеса и предполагая, что в основном масса распределена по ободу, по формуле (5.22) можно определить J k . Для уменьшения ошибки можно утяжелить обод велосипедного колеса, проложив по нему специальные шины. Человек должен располагаться симметрично оси вращения.

Более простой вариант рассмотренной демонстрации состоит в том, что человек, стоящий на скамье Жуковского, сам приводит во вращение колесо, которое он держит на вертикальной оси. При этом человек и платформа начинают вращаться в противоположные стороны (рис. 5.15).

5.4. ПОНЯТИЕ О СВОБОДНЫХ ОСЯХ ВРАЩЕНИЯ

Тело, вращающееся вокруг фиксированной оси, в общем случае действует на подшипники или другие устройства, которые сохраняют неизменным положение этой оси. При больших угловых скоростях и моментах инерции эти воздействия могут быть значительными. Однако в любом теле можно выбрать такие оси, направление которых при вращении будет сохраняться без каких-либо специальных устройств. Чтобы понять, какому условию должен удовлетворять выбор таких осей, рассмотрим следующий пример.

Сопоставляя (5.43) с координатами центра масс, замечаем, что силы, действующие на ось, уравновешиваются, если ось вращения проходит через центр масс.

Таким образом, если ось вращения проходит перпендикулярно стержню через центр масс, то воздействия на эту ось со стороны вращающегося тела не будет. Если при этом убрать подшипники, то ось вращения начнет перемещаться, сохраняя неизменным положение в пространстве, а тело будет продолжать вращение вокруг этой оси.

Оси вращения, которые без специального закрепления сохраняют свое направление в пространстве, называют свободными. Примерами таких осей являются оси вращения Земли и волчка, ось всякого брошенного и свободно вращающегося тела и т.п.

У тела произвольной формы всегда имеется по крайней мере три взаимно перпендикулярные оси, проходящие через центр масс, которые могут быть свободными осями вращения. Эти оси называют главными осями инерции. Хотя все три главные оси инерции являются свободными, наиболее устойчивым будет вращение вокруг оси с наибольшим моментом инерции. Дело в том, что в результате неизбежного действия внешних сил, например трения, а также в связи с тем, что трудно задать вращение точно вокруг определенной оси, вращение вокруг остальных свободных осей неустойчиво.

В некоторых случаях, когда тело вращается около свободной оси с малым моментом инерции, оно само изменяет эту ось на ось с наибольшим моментом.

Это явление демонстрируют следующим опытом. К электродвигателю подвешена на нити цилиндрическая палочка, которая может вращаться вокруг своей геометрической оси (рис. 5.17, а). Момент инерции относительно этой оси J 1 = тR 2 /2. При достаточно большой угловой скорости палочка изменит свое положение (рис. 5.17, б). Момент инерции относительно новой оси равен J 2 = ml 2 /12. Если l 2 >6R 2 , то и J 2 > J 1 . Вращение вокруг новой оси будет устойчивым.

Читатель может самостоятельно на опыте убедиться, что вращение брошенной спичечной коробки устойчиво относительно оси, проходящей перпендикулярно большей грани, и неустойчиво или менее устойчиво относительно осей, проходящих перпендикулярно другим граням (см. рис. 5.8).

Вращение животных и человека в свободном полете и при различных прыжках происходит вокруг свободных осей с наибольшим или наименьшим моментом инерции. Так как положение центра масс зависит от позы тела, то при разных позах будут и различные свободные оси.

5.5. ПОНЯТИЕ О СТЕПЕНЯХ СВОБОДЫ

Положение свободной материальной точки в пространстве задается тремя независимыми координатами: х, у, z. Если точка не свободна, а перемещается, например, по некоторой поверхности, то не все три координаты будут независимыми.

Независимые переменные, характеризующие положение механической системы, называют степенями свободы.

У свободной материальной точки три степени свободы, в рассмотренном примере - две степени свободы. Так как молекулу одноатомного газа можно рассматривать как материальную точку, следовательно, такая свободная молекула тоже имеет три степени свободы.

Еще некоторые примеры.

Две материальные точки 1 и 2 жестко связаны друг с другом. Положение обеих точек задано шестью координатами x 1 , y 1 , z 1 , x 2 , y 2 , z 2 , на которые наложены одно ограничение и одна связь, математически выражаемая в форме уравнения:

Физически это означает, что расстояние между материальными точками всегда l. В этом случае число степеней свободы равно 5. Рассмотренный пример является моделью двухатомной молекулы.

Три материальные точки 1, 2 и 3 жестко связаны друг с. другом. Девять координат характеризуют положение такой системы: x 1 , y 1 , z 1 , x 2 , y 2 , z 2 , x 3 , y 3 , z 3 . Однако три связи между точками обусловливают независимость только шести координат. Система имеет шесть степеней свободы. Так как положение трех точек, не лежащих на одной прямой, однозначно определяет положение твердого тела, то и твердое тело имеет шесть степеней свободы.

Такое же число степеней свободы (шесть) имеют трехатомные и многоатомные молекулы, если эти молекулы рассматривать как жесткие образования.

1 Если для зависимой координаты из (5.44) получают мнимую величину, это означает, что выбранные независимые координаты не соответствуют каким-либо точкам, расположенным на сфере заданного радиуса.

В реальных многоатомных молекулах атомы находятся в колебательных движениях, поэтому число степеней свободы таких молекул более шести.

Число степеней свободы определяет не только число независимых переменных, характеризующих положение механической системы, но и, что очень важно, число независимых перемещений системы. Так, три степени свободы свободной материальной точки означают, что любое перемещение точки можно разложить на независимые перемещения по трем осям координат. Так как точка не имеет размеров, то говорить о ее вращении не имеет смысла. Итак, материальная точка имеет три степени свободы поступательного движения. Материальная точка на плоскости, сфере или иной поверхности имеет две степени свободы поступательного движения. Перемещение материальной точки вдоль кривой (условный пример - движение поезда по рельсам) соответствует одной степени свободы поступательного движения.

Твердое тело, вращающееся вокруг неподвижной оси, имеет одну степень свободы вращательного движения. Колесо поезда имеет две степени свободы: одна - вращательного движения, а другая - поступательного (перемещение оси колеса вдоль рельса). Шесть степеней свободы твердого тела означают, что любое перемещение этого тела можно разложить на составляющие: перемещение центра масс раскладывается на три поступательных движения по осям координат, а вращение состоит из трех более простых поворотов относительно осей координат, проходящих через центр масс.

На рис. 5.18-5.20 показаны шарнирные соединения, соответствующие одной, двум и трем степеням свободы.

Рис. 5.18

Рис. 5.19

Рис. 5.20

5.6. ЦЕНТРИФУГИРОВАНИЕ

Центрифугированием называется процесс разделения (сепарации) неоднородных систем, например частиц от жидкостей, в которых они находятся, обусловленный их вращением.

Рассмотрим разделение неоднородных систем в поле силы тяжести. Предположим, что имеется водная суспензия частиц различной плотности. Со временем благодаря действию силы тяжести и выталкивающей силы F A происходит расслаивание частиц: частицы с большей, чем у воды, плотностью тонут, частицы с меньшей, чем у воды, плотностью всплывают. Результирующая сила, действующая, например, на более плотную отдельную частицу, равна:

где ρ 1 - плотность вещества частицы; ρ - плотность воды; V - объем частицы.

Если значения ρ 1 и ρ мало отличаются друг от друга, то сила F p мала и расслоение (осаждение) происходит достаточно медленно. В центрифуге (сепараторе) такое разделение производят принудительно, вращая разделяемую среду.

Рассмотрим физику этого явления.

Пусть рабочий объем центрифуги (рис. 5.21: а - внешний вид; б - схема рабочего объема) полностью занят какой-либо однородной жидкостью. Выделим мысленно небольшой объем V этой жидкости, находящийся на расстоянии r от оси вращения OO". При равномерном вращении центрифуги на выделенный объем кроме силы тяжести и выталкивающей силы, которые уравновешивают друг друга, действует центростремительная сила. Это сила со стороны окружающей объем жидкости. Она, естественно, направлена к оси вращения и равна:

где ρ - плотность жидкости.

Предположим теперь, что выделенный объем V - это сепарируемая частица, плотность вещества которой ρ 1 (ρ 1 Φ ρ). Сила, действующая на частицу со стороны окружающей жидкости, не изменится, как это видно из формулы (5.45).

Для того чтобы частица вращалась вместе с жидкостью, на нее должна действовать центростремительная сила, равная:

где m 1 - масса частицы, а ρ 1 - соответствующая ей плотность.

Рис. 5.21

Если F > F 1 , то частица перемещается к оси вращения. Если F < F 1 , то воздействия на частицу со стороны жидкости будет недостаточно, чтобы удержать ее на круговой траектории, и частица по инерции начнет перемещаться к периферии. Эффект сепарации определяется превышением силы F, действующей со стороны жидкости на выделенную частицу, над тем значением центростремительной силы F 1 , которое обусловливает движение по окружности:

Это выражение показывает, что эффект центрифугирования тем больше, чем больше различие плотностей сепарируемых частиц и жидкости, а также существенно зависит от угловой скорости вращения 1 .

Сравним разделение центрифугированием с разделением с помощью силы тяжести:

1 Сила тяжести и выталкивающая сила при выводе формулы (5.47) не учитываются, так как они направлены вдоль оси вращения и не оказывают принципиального влияния на центрифугирование.

Ультрацентрифуги способны разделить частицы размером менее 100 нм, взвешенные или растворенные в жидкости. Они нашли широкое применение в медико-биологических исследованиях для разделения биополимеров, вирусов и субклеточных частиц.

Быстрота сепарации особенно важна в биологических и биофизических исследованиях, так как со временем может существенно измениться состояние изучаемых объектов.

План лекции

Момент инерции.

Момент силы. Основное уравнение динамики вращательного движения.

Момент импульса. Закон сохранения момента импульса.

Работа и кинетическая энергия при вращательном движении.

1. Момент инерции.

При рассмотрении вращательного движения необходимо ввести новые физические понятия: момент инерции, момент силы, момент импульса.

Момент инерции является мерой инертности тела при вращательном движении тела.

Момент инерции материальной точки относительно неподвижной оси вращения равен произведению её массы на квадрат расстояния до рассматриваемой оси вращения (рис.1):

зависит только от массы материальной точки и её положения относительно оси вращения и не зависит от наличия самого вращения.

Момент инерции - скалярная и аддитивная величина, поэтому момент инерции тела равен сумме моментов инерции всех его точек:

.

В случае непрерывного распределения массы эта сумма сводится к интегралу:

,

где - масса малого объема тела
,  плотность тела, - расстояние от элемента
до оси вращения.

Момент инерции является аналогом массы при вращательном движении. Чем больше момент инерции тела, тем труднее изменить угловую скорость вращаемого тела. Момент инерции имеет смысл только при заданном положении оси вращения. Бессмысленно говорить просто о “моменте инерции”. Он зависит:

1)от положения оси вращения;

2)от распределения массы тела относительно оси вращения, т.е. от формы тела и его размеров.

Экспериментальным доказательством этого является опыт со скатывающимися цилиндрами.

Произведя интегрирование для некоторых однородных тел, можно получить следующие формулы (ось вращения проходит через центр масс тела).

Момент инерции обруча (толщиной стенок пренебрегаем) или полого цилиндра:

Момент инерции диска или сплошного цилиндра радиуса R:

.

Момент инерции шара

Момент инерции стержня

Если для тела известен момент инерции относительно оси, проходящей через центр масс, то момент инерции относительно любой оси, параллельной первой, находится по теореме Штейнера : момент инерции тела относительно произвольной оси равен моменту инерции J 0 относительно оси, параллельной данной и проходящей через центр масс тела, сложенному с произведением массы тела на квадрат расстояния между осями.

где d расстояние от центра масс О до оси вращения (рис.2).

Центр масс - воображаемая точка, положение которой характеризует распределение массы данного тела. Центр масс тела движется так же, как двигалась бы материальная точка той же массы под действием всех внешних сил, действующих на данное тело.

Понятие момента инерции было введено в механику отечественным ученым Л. Эйлером в середине XVIII века, и с тех пор широко используется при решении многих задач динамики твердого тела. Значение момента инерции необходимо знать на практике при расчете различных вращающихся узлов и систем (маховиков, турбин, роторов электродвигателей, гироскопов). Момент инерции входит в уравнения движения тела (корабля, самолета, снаряда, и т.п.). Его определяют, когда хотят узнать параметры вращательного движения летательного аппарата вокруг центра масс при действии внешнего возмущения (порыва ветра и т.п.).

Сила трения всегда направлена вдоль поверхности соприкосновения в сторону, противоположную движению. Она всегда меньше силы нормального давления.

Здесь:
F - гравитационная сила, с которой два тела притягиваются друг к другу (Ньютон),
m 1 - масса первого тела (кг),
m 2 - масса второго тела (кг),
r - расстояние между центрами масс тел (метр),
γ - гравитационная постоянная 6.67 · 10 -11 (м 3 /(кг · сек 2)),

Напряжённость гравитацио́нного по́ля - векторная величина, характеризующая гравитационное поле в данной точке и численно равная отношению силы тяготения, действующей на тело, помещённое в данную точку поля, к гравитационной массе этого тела:

12. Изучая механику твердого тела, мы использовали понятие абсолютно твердого тела. Но в природе не существует абсолютно твердых тел, т.к. все реальные тела под действием сил изменяют свою форму и размеры, т. е. деформируются .
Деформация называется упругой , если после того, как на тело перестали действовать внешние силы тело восстанавливает первоначальные размеры и форму. Деформации, сохраняющиеся в теле после прекращения действия внешних сил, называютсяпластическими (или остаточными )

РАБОТА И МОЩНОСТЬ

Работа силы.
Работа постоянной силы, действующей на прямолинейно движущееся тело
, где - перемещение тела, - сила, действующая на тело.

В общем случае, работа переменной силы, действующей на тело, движущееся по криволинейной траектории . Работа измеряется в Джоулях [Дж].

Работа момента сил, действующего на тело, вращающееся вокруг неподвижной оси , где - момент силы, - угол поворота.
В общем случае .
Совершенная нат телом работа переходит в его кинетическую энергию.
Мощность - это работа за единицу времени (1 с): . Мощность измеряется в Ваттах [Вт].

14.Кинети́ческая эне́ргия - энергия механической системы, зависящая от скоростей движения её точек. Часто выделяют кинетическую энергию поступательного и вращательногодвижения.

Рассмотрим систему, состоящую из одной частицы, и запишем второй закон Ньютона:

Есть результирующая всех сил, действующих на тело. Скалярно умножим уравнение на перемещение частицы . Учитывая, что , Получим:

Если система замкнута, то есть , то , а величина

остаётся постоянной. Эта величина называется кинетической энергией частицы. Если система изолирована, то кинетическая энергия является интегралом движения.

Для абсолютно твёрдого тела полную кинетическую энергию можно записать в виде суммы кинетической энергии поступательного и вращательного движения:

Масса тела

Скорость центра масс тела

Момент инерции тела

Угловая скорость тела.

15.Потенциальная энергия - скалярная физическая величина, характеризующая способность некого тела (или материальной точки) совершать работу за счет своего нахождения в поле действия сил.

16. Растяжение или сжатие пружины приводит к запасанию ее потенциальной энергии упругой деформации. Возвращение пружины к положению равновесия приводит к высвобождению запасенной энергии упругой деформации. Величина этой энергии равна:

Потенциальная энергия упругой деформации..

- работа силы упругости и изменение потенциальной энергии упругой деформации.

17.консервати́вные си́лы (потенциальные силы) - силы, работа которых не зависит от формы траектории (зависит только от начальной и конечной точки приложения сил) . Отсюда следует определение: консервативные силы - такие силы, работа которых по любой замкнутой траектории равна 0

Диссипати́вные си́лы - силы, при действии которых на механическую систему её полная механическая энергия убывает (то есть диссипирует), переходя в другие, немеханические формы энергии, например, в теплоту.

18. Вращением вокруг неподвижной оси называется такое движение твердого тела, при котором во все время движения две его точки остаются неподвижными. Прямая, проходящая через эти точки, называется осью вращения. Все остальные точки тела движутся в плоскостях, перпендикулярных оси вращения, по окружностям, центры которых лежат на оси вращения.

Момент инерции - скалярная физическая величина, мера инертности во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле: момент инерции равен сумме произведений элементарных масс на квадрат их расстояний до базового множества (точки, прямой или плоскости).

Моментом инерции механической системы относительно неподвижной оси («осевой момент инерции») называется величина J a , равная сумме произведений масс всех n материальных точек системы на квадраты их расстояний до оси:

,

§ m i - масса i -й точки,

§ r i - расстояние от i -й точки до оси.

Осевой момент инерции тела J a является мерой инертности тела во вращательном движении вокруг оси подобно тому, как масса тела является мерой его инертности в поступательном движении.

,

§ - масса малого элемента объёма тела ,

4.6 Вращательное движение твердого тела. Момент силы.

Конечно, положение одной, даже «особой», точки далеко не полностью описывает движение всей рассматриваемой системы тел, но все-таки, лучше знать положение хотя бы одной точки, чем не знать ничего. Тем не менее, рассмотрим применение законов Ньютона к описанию вращения твердого тела вокруг фиксированной оси .

Начнем с простейшего случая: пусть материальная точка массы m прикреплена с помощью невесомого жесткого стержня длиной r к неподвижной оси OO’ (рис. 46). Материальная точка может двигаться вокруг оси, оставаясь от нее на постоянном расстоянии, следовательно, ее траектория будет являться окружностью с центром на оси вращения.

Безусловно, движение точки подчиняется уравнению второго закона Ньютона \(~m \vec a = \vec F_0\). Однако, непосредственное применение этого уравнения не оправдано: во-первых, точка обладает одной степенью свободы, поэтому в качестве единственной координаты удобно использовать угол поворота, а не две декартовые координаты; во-вторых, на рассматриваемую систему действуют силы реакции в оси вращения, а непосредственно на материальную точку – сила натяжения стержня. Нахождение этих сил представляет собой отдельную проблему, решение которой излишне для описания вращения. Поэтому имеет смысл получить на основании законов Ньютона специальное уравнение, непосредственно описывающее вращательное движение.

Пусть в некоторый момент времени на материальную точку действует некоторая сила \(~\vec F\), лежащая в плоскости перпендикулярной оси вращения (рис. 47). При кинематическом описании криволинейного движения вектор полного ускорения \(~\vec a\) удобно разложить на две составляющих: нормальную \(~\vec a_n\), направленную к оси вращения, и тангенциальную \(~\vec a_{\tau}\) , направленную параллельно вектору скорости. Значение нормального ускорения для определения закона движения нам не нужно. Конечно, это ускорение также обусловлено действующими силами, одна из которых неизвестная сила натяжения стержня.

Запишем уравнение второго закона в проекции на тангенциальное направление:

\(~m a_{\tau} = F_{\tau}\) , (1)

заметим, что сила реакции стержня не входит в это уравнение, так как она направлена вдоль стержня и перпендикулярна выбранной проекции. Изменение угла поворота φ непосредственно определяется угловой скоростью \(~\omega = \frac{\Delta \varphi}{\Delta t}\) , изменение которой в свою очередь описывается угловым ускорением \(~\varepsilon = \frac{\Delta \omega}{\Delta t}\) . Угловое ускорение связано с тангенциальной составляющей ускорения соотношением a τ = rε . Если подставить это выражение в уравнение (9), то получим уравнение, пригодное для определения углового ускорения. Удобно ввести новую физическую величину, определяющую взаимодействие тел при их повороте. Для этого умножим обе части уравнения (1) на r

\(~m r^2 \varepsilon = F_{\tau} r\) . (2)

и рассмотрим выражение в его правой части F τ r , имеющего смысл произведения тангенциальной составляющей силы, на расстояние от оси вращения до точки приложения силы. Это же произведение можно представить несколько иной форме (см. рис. 48)

M = F τ r = Fr cos α = Fd , здесь d - расстояние от оси вращения до линии действия силы, которое также называют плечом силы . Эта физическая величина, произведение модуля силы на расстояние от линии действия силы до оси вращения (плечо силы) M = Fd называется моментом силы . Действие силы может приводить к вращению, как по часовой стрелке, так и против часовой стрелки. В соответствии с выбранным положительным направлением вращения следует определять и знак момента силы. Заметьте, что момент силы определяется той составляющей силы, которая перпендикулярна радиус-вектору точки приложения. Составляющая вектора силы, направленная вдоль отрезка, соединяющего точку приложения и ось вращения, не приводит к раскручиванию тела. Эта составляющая при закрепленной оси компенсируется силой реакции в оси, поэтому она не влияет на вращение тела.

Запишем еще одно полезное выражения для момента силы. Пусть сила \(~\vec F\) приложена к точке А , декартовые координаты которой равны x ,y (рис. 49). Разложим силу \(~\vec F\) на две составляющие \(~\vec F_x, \vec F_y\) , параллельные соответствующим осям координат. Момент силы \(~\vec F\) относительно оси, проходящей через начало координат, очевидно равен сумме моментов составляющих \(~\vec F_x, \vec F_y\) , то есть M = xF y - yF x .

Аналогично, тому, как нами было введено понятие вектора угловой скорости, можно определить также и понятие вектора момента силы. Модуль этого вектора соответствует данному выше определению, направлен же он перпендикулярно плоскости, содержащей вектор силы и отрезок, соединяющий точку приложения силы с осью вращения. Вектор момента силы также может быть определен как векторное произведение радиус-вектора точки приложения силы на вектор силы

\(~\vec M = \vec r \times \vec F\) .

Заметим, что при смещении точки приложения силы вдоль линии ее действия момент силы не изменяется.

Обозначим произведение массы материальной точки на квадрат расстояния до оси вращения mr 2 = I (эта величина называется моментом инерции материальной точки относительно оси ). С использованием этих обозначений уравнение (2) приобретает вид, формально совпадающий с уравнением второго закона Ньютона для поступательного движения

\(~I \varepsilon = M\) . (3)

Это уравнение называется основным уравнением динамики вращательного движения. Итак, момент силы во вращательном движении играет такую же роль, как и сила в поступательном движении, именно он определяет изменение угловой скорости. Оказывается, (и это подтверждает наш повседневный опыт) влияние силы на скорость вращения определяет не только величина силы, но и точка его приложения. Момент инерции определяет инерционные свойства тела по отношению к вращению (говоря простым языком – показывает, легко ли раскрутить тело) - чем дальше от оси вращения находится материальная точка, тем труднее привести ее во вращение.

Уравнение (3) допускает обобщение на случай вращения произвольного тела. При вращении тела вокруг фиксированной оси угловые ускорения всех точек тела одинаковы. Поэтому, аналогично тому, как мы проделали при выводе уравнения Ньютона для поступательного движения тела, можно записать уравнения (3) для всех точек вращающегося тела и затем их просуммировать. В результате мы получим уравнение, внешне совпадающее с (3), в котором I - момент инерции всего тела, равный сумме моментов составляющих его материальных точек, M - сумма моментов внешних сил, действующих на тело.

Покажем, каким образом вычисляется момент инерции тела. Важно подчеркнуть, момент инерции тела зависит не только от массы, формы и размеров тела, но и от положения и ориентации оси вращения. Формально процедура расчета сводится к разбиению тела на малые части, которые можно считать материальными точками (рис. 51), и суммированию моментов инерций этих материальных точек, которые равны произведению массы на квадрат расстояния до оси вращения

\(~I = m_1 r^2_1 + m_2 r^2_2 + m_3 r^2_3 + \ldots\) .

Для тел простой формы такие суммы давно подсчитаны, поэтому часто достаточно вспомнить (или найти в справочнике) соответствующую формулу для нужного момента инерции. В качестве примера: момент инерции кругового однородного цилиндра массы m и радиуса R для оси вращения совпадающей с осью цилиндра равен \(~I = \frac{1}{2} m R^2\) .

Из всех видов вращательного движения будем рассматривать только вращение тела вокруг неподвижной оси.

Момент силы

Момент силы, величина, характеризующая вращательный эффект силы при действии её на твёрдое тело; является одним из основных понятий механики. Различают момент силы относительно центра (точки –полюса) и относительно оси.

Моментом силы (синонимы: крутящий момент, вращательный момент, вертящий момент, вращающий момент ) относительно неподвижной точки 0 (полюса ) называется векторная величина равная векторному произведению радиус – вектора проведённого из точки 0 (полюса ) в точку А приложения силы, на вектор силы : .

Модуль момента силы: , где: – момент силы, – приложенная сила, – расстояние от центра вращения до места приложения силы, . – плечо силы, т.е. длина перпендикуляра, опущенного из центра вращения на линию действия силы , – угол, между вектором силы и вектором положения . Т.е. численно момент силы равен произведению модуля силы на плечо .

Направление момента силы можно также определить по правилу левой руки: четыре пальца левой руки поставить по направлению первого сомножителя , второй сомножитель входит в ладонь, отогнутый под прямым углом большой палец укажет направления момента силы . Вектор момента силы всегда перпендикулярен плоскости, в которой лежат векторы и .

Рис. 68.

Моментом силы относительно неподвижной оси называется скалярная величина равнаяпроекции на эту ось вектора момента силы , определённого относительно произвольной точки данной оси (рис. 68). Момент силы относительно оси величина алгебраическая.

Пользуясь понятием момента силы можно по-новому сформулировать условия равновесия тела, закрепленного на оси. Это условие называется правилом моментов:если на тело, закрепленное на оси, действует много сил, то для равновесия тела, закрепленного на оси, алгебраическая сумма моментов всех сил, действующих на тело, должна быть равна нулю :

Рис. 69.

Считают момент силы положительным , если эта сила, действуя в отдельности, вращала бы тело по часовой стрелке, и отрицательным в противоположном случае (при этом нужно заранее условиться, с какой стороны мы будем смотреть на тело). Например, согласно рис.69, силам и следует приписать положительный момент, а силе – отрицательный.

Примеры:

1). Гаечный ключ

Рис. 70.

2). Пусть на тело, в плоскости перпендикулярной оси вращения действует сила . Разложим эту силу на две составляющие: и .(рис. 70).

Сила пересекает ось вращения и, следовательно, не влияет на вращение тела. Под действием составляющей тело будет совершать вращательное движение вокруг оси . Расстояние от оси вращения до линии вдоль которой действует сила ,называется плечом силы . Моментом силы относительно точки 0 называется произведение модуля силы на плечо : .

С учетом, что ,момент силы С точки зрения векторной алгебры это выражение представляет векторное произведение радиуса-вектора проведенного в точку приложения силы на эту силу.

Таким образом, момент силы относительно точки 0 является векторной величиной и равен: .

Вектор момента силы направлен перпендикулярно к плоскости, проведенной через векторы и , и образует с ними правую тройку векторов (при наблюдении из вершины вектора видно, что вращение по кратчайшему расстоянию от к происходит против часовой стрелки).

Примеры:

1). Рычаги

Рычагом называют имеющее неподвижную ось вращения твердое тело, на которое действуют силы, стремящиеся повернуть его вокруг этой оси.

Примерами рычагов являются гаечные ключи, различные педали, щипцы для раскалывания орехов, двери и т. д.

Согласно правилу моментов, рычаг (любого рода) уравновешен только тогда, когда . Поскольку и , получаем . Из последней формулы следует, что:

т. е., при равновесии рычага под действием двух сил модули этих сил обратно пропорциональны их плечам. Т.е. с помощью рычага можно получить выигрыш в силе тем больший, чем больше соотношение плеч. Это широко используют на практике.

2). Пара сил

Рис. 71.

Две равные по модулю антипараллельные силы, приложенные к телу в разных точках, называют парой сил. Примерами пары сил могут служить силы, которые приложены к рулевому колесу автомобиля (рис.71а ), электрические силы, действующие на диполь (рис.71б ), магнитные силы, действующие на магнитную стрелку (рис. 71в ) и т. д.

Пара сил не имеет равнодействующей, т. е. совместное действие этих сил нельзя заменить действием одной силы. Поэтому пара сил не может вызвать поступательное движение тела, а вызывает только его вращение.

Если при повороте тела под действием пары сил направления этих сил не изменяются (рис.71б, в ), то поворот тела происходит до тех пор, пока обе силы не окажутся действующими противоположно друг другу вдоль прямой, проходящей через ось вращения тела.

Пусть на тело, имеющее закрепленную ось вращения О, действует пара сил и . Моменты этих сил и (рис. 72). Сумма моментов , следовательно, тело не находится в равновесии.

Рис. 72.

Кратчайшее расстояние между параллельными прямыми, вдоль которых действуют силы, образующие пару сил, называют плечом пары сил : –это момент пары сил. Следовательно, момент пары сил равен произведению модуля одной из сил этой пары на плечо пары независимо от положения оси вращения тела при условии, что эта ось перпендикулярна плоскости, в которой находится пара сил.

Если пара сил действует на тело, не имеющее закрепленную ось вращения, она вызывает вращение этого тела вокруг оси, проходящей через центр масс данного тела.

Момент импульса

Моме́нт и́мпульса (кинетический момент, угловой момент, орбитальный момент, момент количества движения) характеризует количество вращательного движения. Величина, зависящая от того, сколько массы вращается, как она распределена относительно оси вращения и с какой скоростью происходит вращение.

Следует учесть, что вращение здесь понимается в широком смысле, не только как регулярное вращение вокруг оси. Например, даже при прямолинейном движении тела мимо произвольной воображаемой точки, не лежащей на линии движения, оно также обладает моментом импульса. Наибольшую, пожалуй, роль момент импульса играет при описании собственно вращательного движения. Однако крайне важен и для гораздо более широкого класса задач (особенно – если в задаче есть центральная или осевая симметрия, но не только в этих случаях).

Рис. 73.

Момент импульса материальной точки относительно некоторого начала отсчёта (т.О – полюс) определяется векторным произведением её радиус-вектора и импульса (рис. 73):

,

где –радиус-вектор частицы относительно выбранного неподвижного в данной системе отсчёта начала отсчёта, –импульс частицы.

Модуль момента импульса равен: , где – плечо импульса, точка 0 – полюс, точка – точка приложения вектора импульса .

Так как момент импульса определяется векторным произведением, он является псевдовектором, перпендикулярным обоим векторам и . Однако, в случаях вращения вокруг неизменной оси, бывает удобно рассматривать не момент импульса как псевдовектор, а его проекцию на ось вращения как скаляр, знак которого зависит от направления вращения.

Если выбрана такая ось, проходящая через начало отсчёта, для вычисления проекции углового момента на нее можно указать ряд приемов в соответствии с общими правилами нахождения векторного произведения двух векторов:

,

Рис. 74.

где – угол между и , определяемый так, чтобы поворот от к производился против часовой стрелки с точки зрения наблюдателя, находящегося на положительной части оси вращения (рис. 74). Направление поворота важно при вычислении, так как определяет знак искомой проекции.

Из определения момента импульса следует его аддитивность. Для нескольких частиц момент импульса определяется как (векторная) сумма таких членов: , где и – радиус-вектор и импульс каждой частицы, входящей в систему, момент импульса которой определяется.В случае твёрдого тела задача сводится к интегрированию: .

Пример:

Момент импульса материальной точки массой , вращающейся по окружности радиусом (рис. 75): .

Важнейшим законом природы является закон сохранения момента импульса :в инерциальной системе отсчёта момент импульса замкнутой системы частиц остаётся постоянным : .

Как доказано в современной физике (теорема Э.Нетер) закон сохранения момента импульса – следствие изотропности пространства .

Момент инерции

Известно, что твёрдое тело при вращении приобретает определённую устойчивость (катящиеся монета, обруч).

По аналогии с первым законом Ньютона можно утверждать:

Твёрдое тело, вращающееся вокруг некоторых осей, проходящих через центр масс, не испытывает действия внешних сил и сохраняет вращение неопределённо долго.

Рис. 76.

Пусть –тая материальная точка массой вращается по окружности радиуса под действием силы (рис. 76).

Тогда по второму закону Ньютона: , , где –угловое ускорение точки; отсюда следует: , где – момент силы относительно оси вращения.

Обозначим: – момент инерции вращающейся точки.

Тогда момент силы действующий на точку: .

Момент инерции тела относительно оси вращения равен сумме моментов инерции всех его точек: . Математически задача сводится к интегрированию.

Момент инерцииI –скалярная величина, характеризующая распределение масс в теле и являющаяся наряду с массой мерой инертности тела во вращательном движении .

Одно и то же тело может иметь различные моменты инерции относительно разных осей.

При заданном относительно тела направлении оси момент инерции тела относительно этой оси будет наименьшим , если ось проходит через центр масс тела (т. С) , т.е. .

Среди осей, проходящих через центр масс тела, имеются три особые взаимно перпендикулярные оси. При равномерном вращении вокруг этих осей тело не оказывает влияния на подшипники. Эти оси называются главными осями . При произвольной форме тела нахождение их затруднительно. Но у симметричных тел положение главных осей определяется легко. Моменты инерции тела относительно главных осей называются главными моментами инерции.

Главные моменты инерции тел простой формы

Моменты инерции однородных тел простейшей формы относительно некоторых осей вращения
Тело	Описание	Положение оси a	Момент инерции
	Материальная точка массы m	На расстоянии r от точки, неподвижная
	Полый тонкостенный цилиндр или кольцо радиуса r и массы m	Ось цилиндра
	Сплошной цилиндр или диск радиуса r и массы m	Ось цилиндра
	Полый толстостенный цилиндр массы m с внешним радиусом r 2 и внутренним радиусом r 1 (труба)	Ось цилиндра
	l и массы m	Ось перпендикулярна к стержню и проходит через его центр масс
	Прямой тонкий стержень длины l и массы m	Ось перпендикулярна к стержню и проходит через его конец
	Тонкостенная сфера радиуса r и массы m	Ось проходит через центр сферы
	Шар радиуса r и массы m	Ось проходит через центр шара

Теорема Штейнера

Момент инерции тела относительно произвольной оси определяется по теореме Штейнера:

Рис. 77.

Момент инерции тела относительно произвольной оси равен сумме момента инерции относительно оси , параллельной данной и проходящей через центр инерции тела , произведения массы тела на квадрат расстояния между осями (рис. 77).

где - произвольная ось, – расстояние между осями.

Математическая формулировка теоремы Штейнера: ,где – масса тела.

Пример.

Момент инерции стержня относительно оси, проходящей через его конец, равен:

где – момент инерции стержня относительно оси, проходящей через центр масс стержня.

Уравнение динамики вращательного движения твёрдого тел относительно неподвижной оси

Из предыдущего параграфа (Момент инерции ) следует, что для вращающейся по окружности - той материальной точки справедливо соотношение: .

Для твёрдого тела, состоящего из материальных точек: ; ,получаем: .

Уравнение (1) – уравнение динамики вращающегося твёрдого тела (основное уравнение динамики вращательного движения):

Угловое ускорение твёрдого тела , вращающегося вокруг неподвижной оси , прямо пропорционально суммарному моменту всех внешних сил , действующих на тело , и обратно пропорционально его моменту инерции.

Представим уравнение (1) в виде:

С учётом того, что , где – момент импульса тела. Тогда: . (2)

Уравнение (2) – так же является уравнением динамики вращающегося твёрдого тела (основное уравнение динамики вращательного движения):

Скорость изменения момента импульса тела относительно некоторой оси равна результирующему моменту относительно той же оси всех внешних сил , приложенных к телу.

Из уравнений (1) и (2) следует: .

Тогда получаем: . (3)

Рис. 78.

Если система частиц замкнута, то на неё внешние силы не действуют, то момент внешних сил ,т.е. получен закон сохранения импульса. С учётом уравнения (3) получаем: . Следовательно, ,т.е.угловая скорость обратно пропорциональна моменту инерции тела(см. рис. 78).

Подобное свойство используется при исполнении фигуристами пируетов на льду, сальто акробатами.

Кинетическая энергия вращающегося твёрдого тела

Вращающееся твёрдое тело обладает энергией.

При вращении твёрдого тела относительно неподвижной оси отдельные его элементы массы описывают окружности различных радиусов и имеют различные линейные скорости . Однако угловая скорость вращения всех точек тела одинакова:

.

Кинетическая энергия тела – сумма кинетических энергий всех его тоек:

.Т.к. , то получаем:

Учтём, что момент инерции тела равен сумме моментов инерции всех его точек: .

С учётом последнего соотношения получаем окончательное выражение для кинетической энергии вращающегося твёрдого тела:

В случае плоского движения твёрдого тела его полная кинетическая энергия равна:

.

Аналогия между поступательным и вращательным движениями

Между движением твердого тела вокруг неподвижной оси и движением отдельной материальной точки (или поступательным движением тела) существует тесная и далеко идущая аналогия. Каждой линейной величине из кинематики точки соответствует подобная величина из кинематики вращения твердого тела. Координате соответствует угол , линейной скорости , угловая скорость , линейному (касательному) ускорению – угловое ускорение .

Поступательное движение	Вращательное движение
Кинематические характеристики движения
Путь	S	м	Угол поворота	j	рад
Время	t	с	Период	Т	с
Скорость		м/с	Угловая скорость	w	рад/с
Ускорение	a	м/с 2	Угловое ускорение	e	рад/с 2
Динамические характеристики движения
Масса	m	кг	Момент инерции	J	кг× м 2
Сила	F	Н	Момент силы	M	Н× м
Импульс	P	кг×м/с	Момент импульса	L=J× w	кг× м 2 /с
Второй закон Ньютона	F=ma; F=dp/dt	Уравнение динамики вращательного движения	M=J×e; M=dL/dt
Работа	dA=F×dS	Дж	Работа	dA=M×dj	Дж
Кинетическая энергия	E K =(m 2)/2	Дж	Кинетическая энергия	E K ВР =(J w 2)/2	Дж
Мощность	N=F	Вт	Мощность	N=М× w	Вт

Поступательное движение можно рассматривать, как вращательное, с радиусом вращения, стремящимся к бесконечности, и угловой скоростью, стремящейся к нулю.

Рис. 79.

5. Механический (классический) принцип относительности

(принцип относительности Галилея)

Краткая биография Г.Галилея

ГАЛИЛЕЙ Галилео (15.II.1564 – 8.I.1642) – выдающийся итальянский физик и астроном, один из основателей точного естествознания, член Академии де Линчей (1611 г.), родился в Пизе. В 1581 г. поступил в Пизанский университет, где изучал медицину. Но, увлекшись геометрией и механикой, в частности сочинениями Архимеда и Евклида, оставил университет с его схоластическими лекциями и вернулся во Флоренцию, где четыре года самостоятельно изучал математику.

С 1589 г.– профессор Пизанского ун-та, в 1592 –1610 гг.– Падуанского, в дальнейшем – придворный философ герцога Козимо II Медичи.

Оказал значительное влияние на развитие научной мысли. Именно от него берет начало физика как наука. Галилею человечество обязано двумя принципами механики, сыгравшими большую роль в развитии не только механики, но и всей физики. Это известный галилеевский принцип относительности для прямолинейного и равномерного движения и принцип постоянства ускорения силы тяжести.

Галилей установил закон инерции (1609), законы свободного падения, движения тела по наклонной плоскости (1604 – 09) и тела, брошенного под углом к горизонту, открыл закон сложения движений и закон постоянства периода колебаний маятника (явление изохронизма колебаний, 1583). От Галилея ведет свое начало динамика.

В июле 1609 г. Галилей построил свою первую подзорную трубу – оптическую систему, состоящую из выпуклой и вогнутой линз, – и начал систематические астрономические наблюдения. Это было второе рождение подзорной трубы, которая после почти 20-летней неизвестности стала мощным инструментом научного познания. Поэтому Галилея можно считать изобретателем первого телескопа. Он достаточно быстро усовершенствовал свою подзорную трубу и, как писал со временем, «построил себе прибор в такой степени чудесный, что с его помощью предметы казались почти в тысячу раз больше и более чем в тридцать раз ближе, чем при наблюдении простым глазом». В трактате «Звездный вестник», вышедшем в Венеции 12 марта 1610 г., он описал открытия, сделанные с помощью телескопа: обнаружение гор на Луне, четырех спутников у Юпитера, доказательство, что Млечный Путь состоит из множества звезд.

Астрономические открытия Галилея сыграли огромную роль в развитии научного мировоззрения, они со всей очевидностью убеждали в правильности учения Коперника, ошибочности системы Аристотеля и Птолемея, способствовали победе и утверждению гелиоцентрической системы мира. В 1632 г. вышел известный «Диалог о двух главнейших системах мира», в котором Галилей отстаивал гелиоцентрическую систему Коперника. Выход книги разъярил церковников, инквизиция обвинила Галилея в ереси и, устроив процесс, заставила публично отказаться от коперниковского учения, а на «Диалог» наложила запрет. После процесса в 1633 г. Галилей был объявлен «узником святой инквизиции» и вынужден был жить сначала в Риме, а затем в Арчертри близ Флоренции. Однако научную деятельность Галилей не прекратил, до своей болезни (в 1637 г. Галилей окончательно потерял зрение) он завершил труд «Беседы и математические доказательства, касающиеся двух новых отраслей науки», который подводил итог его физических исследований.

Изобрел термоскоп, являющийся прообразом термометра, сконструировал (1586 г.) гидростатические весы для определения удельного веса твердых тел, определил удельный вес воздуха. Выдвинул идею применения маятника в часах. Физические исследования посвящены также гидростатике, прочности материалов и т. п.

Сочинения:

1. Диалог о двух главнейших системах мира Птоломеевой и Коперниковой. М.–Л. ОГИЗ, 1948.

2. Пробирных дел мастер / Пер. Ю. А. Данилова. – М.: Наука, 1987. – 272 с. – (Серия «Популярныепроизведения классиков естествознания»).

3. Беседы и математические доказательства, касающиеся двух новых отраслей наук (Сочинения. т.1). ГТТИ. М–Л. 1934.

4. Рассуждения о телах, плавающих в воде, и о тех, которые в ней движутся.В кТ: Архимед. Стэвин. Галилей. Паскаль.Начала гиростатики. Серия "Классики естествознания"» ГНТТИ. М.-Л. 1933.

Механический принцип относительности

Принцип относительности – это принцип равноправия инерциальных систем отсчёта (ИСО) в классической механике, проявляющегося в том, что законы механики во всех таких системах одинаковы, был установлен Г.Галилеем в 1636 г.

Одинаковость законов механики для инерциальных систем Галилей иллюстрировал на примере явлений, происходящих под палубой корабля, покоящегося или движущегося равномерно и прямолинейно (относительно Земли, которую можно с достаточной степенью точности считать инерциальной системой отсчёта): «Заставьте теперь корабль двигаться с любой скоростью и тогда (если только движение будет равномерным и без качки в ту и другую сторону) во всех названных явлениях вы не обнаружите ни малейшего изменения и ни по одному из них не сможете установить, движется ли корабль или стоит неподвижно... Бросая какую-нибудь вещь товарищу, вы не должны будете бросать ее с большей силой, когда он будет находиться на носу, а вы на корме, чем когда ваше взаимное положение будет обратным; капли, как и ранее, будут падать в нижний сосуд, и ни одна не упадет ближе к корме, хотя, пока капля находится в воздухе, корабль пройдет много пядей» («Диалог о двух главнейших системах мира птоломеевой и коперниковой», М. – Л., 1948, с. 147).

Движение материальной точки относительно: её положение, скорость, вид траектории зависят от того, по отношению к какой системе отсчёта (телу отсчёта) это движение рассматривается. В то же время законы классической механики, т. е. соотношения, которые связывают величины, описывающие движение материальных точек и взаимодействие между ними, одинаковы во всех инерциальных системах отсчёта. Относительность механического движения и одинаковость (безотносительность) законов механики в разных инерциальных системах отсчёта и составляют содержание принципа относительности Галилея.Сам принцип логически следует из известных преобразований Галилея.

Преобразова́ния Галиле́я – в классической механике преобразования координат и скорости при переходе от одной инерциальной системы отсчета (ИСО ) к другой .

Эти преобразования справедливы лишь при скоростях много меньше скорости света в вакууме и основываются на двух предположениях, которые принимались неявно и считались очевидными:

Ход времени одинаков во всех инерциальных системах отсчета;

Линейные размеры тела не зависят от скорости его движения относительно системы отсчета.

Рис. 80.

Пусть имеются две инерциальные системы отсчёта, одну из которых, , условимся считать покоящейся; вторая система, , движется по отношению к с постоянной скоростью так, как показано на рис. 80.

Тогда преобразования Галилея имеют вид:

или, используя векторные обозначения,

(последняя формула остается верной для любого направления осей координат).

Из преобразований Галилея следуют:

Классический закон сложения скоростей: где – скорость точки М в «неподвижной» системе отсчета , ’ – скорость точки М в движущейся системе ;

Инвариантность (неизменность) ускорения точки М и сил, действующих на неё:

Из последних соотношений следует, что уравнение второго закона Ньютона не изменяется при переходе от одной ИСО к другой, т.е. законы Ньютона инвариантны к преобразованиям Галилея.

Современные формулировки классического принципа относительности:

1). Во всех ИСО при одних и тех же условиях все механические явления протекают одинаково.

2). Законы классической механики инвариантны относительно перехода их одной ИСО в другую.

В современной физике показано, что классический принцип относительности свидетельствует о том, что все ИСО равноправны, «абсолютной» системы отсчета нет.

Принцип относительности Галилея справедлив лишь в классической механике, в которой рассматриваются движения со скоростями, много меньшими скорости света. При скоростях, близких к скорости света, движение тел подчиняется законам релятивистской механики Эйнштейна, которые инвариантны по отношению к другим преобразованиям координат и времени Лоренца. Одним из постулатов специальной теории стал сформулированный Эйнштейном релятивистский принцип относительности : законы физики инвариантны относительно перехода из одной ИСО в другую.